This article was written solely for informational and educational purposes, and does not constitute medical advice. If you have any health concerns, please consult a qualified medical professional.
Patients and medical professionals are often interested in the probability that an event will or will not have occurred after a certain amount of time. For example, what is the probability that a burn will have healed after two weeks? What is the probability that someone’s cancer will not have returned five years after they have gone into remission? To estimate these probabilities, researchers use a branch of statistics known as survival analysis.
Survival analysis is the study of time to event data. These are data that for each subject measure the time that elapses from a defined starting point – for example, the diagnosis of a disease – until a particular event happens – for example, death. Despite the name, survival analysis does not presume that this event is death – indeed, it could be a positive event, such as discharge from hospital. Though commonly used in medical statistics, survival analysis is not exclusive to epidemiology. It is also employed in fields as diverse as engineering and sociology, meaning it is sometimes known by other names, such as ‘reliability analysis’1.
One of the central tasks of survival analysis is to estimate the survival function, \(S(t)\), for the event of interest. This is a function of time equal to the probability that the event takes longer than the input time, \(t\), to occur
Let’s consider a very simple scenario in which we might estimate a survival function. Suppose an electrical manufacturing company has a batch of faulty light bulbs, and they decide to pick ten of them at random to leave on and monitor for a week. They observe that:
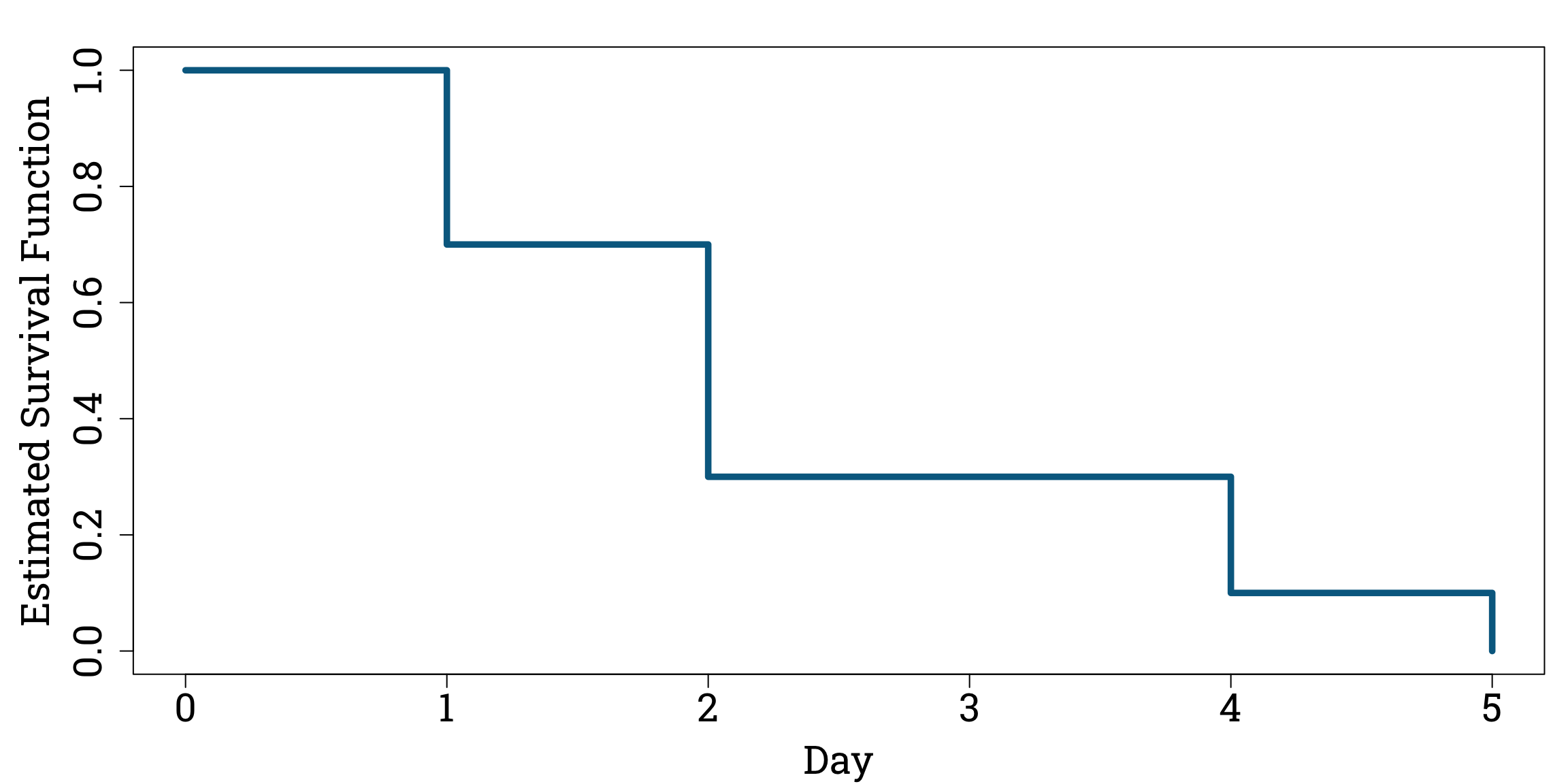
Putting aside the fact that this is a very small sample, it is relatively straightforward to estimate the survival function for these faulty light bulbs from this experiment. For example, to estimate \(S(1)\), we just look at the proportion of light bulbs that last longer than one day – seven tenths. By the law of large numbers, as we increase the number of light bulbs in the sample this proportion will eventually converge to the true probability of a faulty light bulb lasting longer than one day. We can do this calculation for each time marker, including the start point of the experiment – we call this Day 0.
| Day | Survival Function Estimate |
| 0 | \(1\) |
| 1 | \(\frac{7}{10}\) |
| 2 | \(\frac{3}{10}\) |
| 3 | \(\frac{3}{10}\) |
| 4 | \(\frac{1}{10}\) |
| 5 | \(0\) |
days <- 0:5 # creating a vector of time markers
survival_function <- c(1, 7/10, 3/10, 3/10, 1/10, 0) # creating a vector of estimated probabilities
par(mar=c(bottom=4.2, left=5.1, top=1.8, right=0.9), family="Roboto Slab") # setting the plot options
plot(days, survival_function, type="s", ylim=c(0,1), xlab="Day", ylab="Estimated Survival Function", col="#006a90", lwd=4.8, cex.lab=1.8, cex.axis=1.8)
Easy, right? Unfortunately, the time to event data we find in medical applications are rarely this straightforward to work with.
In many medical studies producing time to event data, patients are recruited over a period of some time and then followed until a defined end date, at which point the investigators will want to analyse their outcomes. As a result of this, the event of interest may not have happened for all the subjects of the study. In survival analysis, these ‘incomplete’ data points are known as censored data. They do give us some information – we know the event we are studying had not yet happened at the point at which censoring occurred. However, we cannot tell when, or indeed if, it would have gone on to happen.
Censoring can also come about in other ways, including patients being lost to follow up, or experiencing a ‘competing event’2. For example, in a study of the time it took for catheter-associated complications to arise in children undergoing peritoneal dialysis, observations were considered censored when a patient’s catheter was removed before a complication had occurred3.
Censored data make estimating a survival function considerably more complicated. Imagine, for example, that three of the light bulbs in our previous thought experiment accidentally got smashed at the end of the first day.
We could still approximate \(S(1)\) to be seven tenths, since \[\mathbb{P}(T>1)=1-\mathbb{P}(T\leq1),\] which, since three light bulbs fail on the first day, we can estimate to be \[1-\frac{3}{10}=\frac{7}{10},\] as in the original case. But what about \(S(2)\) onwards? We don’t know on which days the smashed light bulbs would have failed, so we can’t estimate \(S(t)\) for these values of \(t\) in the same way.
In 1958, Edward Kaplan and Paul Meier proposed an ingenious solution to the censoring problem4. Their paper has gone on to become the most cited publication in the history of statistics5, and is seen as a seminal contribution to the field of survival analysis. Kaplan and Meier’s central insight was that while censoring may stop us from directly estimating \(\mathbb{P}(T>t_i)\) for a particular value of time, \(t_i\), it does not stop us from estimating \[\mathbb{P}(T>t_i\,|\,T>t_{i-1}),\] This is the conditional probability of an event taking longer than \(t_i\) days, months, or years to occur, given that it has not already happened in \(t_{i-1}\) days, months, or years.
These conditional probabilities are quite easy to find, since
\[\begin{split} \mathbb{P}(T>t_i\,|\,T>t_{i-1})&=1-\mathbb{P}(T\leq t_i\,|\,T>t_{i-1})\\&=1-\mathbb{P}(T=t_i\,|\,T>t_{i-1}). \end{split}\]
which we can estimate by calculating the proportion of subjects remaining in the study (those who have not experienced censoring or the event of interest) after \(t_{i-1}\) that do not have a time to event of \(t_i\).
In our smashed light blub thought experiment, for example, we could estimate \(\mathbb{P}(T>2\,|\,T>1)\) to be two quarters (or one half). This is because on the first day three light bulbs fail and three light bulbs are censored, so four remain in the experiment on the second day, two of which survive
Kaplan and Meier realised that we can get from these conditional probabilities to the survival function using the chain rule of conditional probabilities. For any \(t_i\), we have that
\[ \begin{split} \mathbb{P}(T>t_i) &=\mathbb{P}(T> t_i\,|\,T>t_{i-1})\mathbb{P}(T>t_{i-1})\\ &=\mathbb{P}(T> t_i\,|\,T>t_{i-1})\mathbb{P}(T>t_{i-1}\,|\,T>t_{i-2})\mathbb{P}(T>t_{i-2})\\ &=\mathbb{P}(T> t_i\,|\,T>t_{i-1})\mathbb{P}(T>t_{i-1}\,|\,T>t_{i-2})\mathbb{P}(T>t_{i-2}\,|\,T>t_{i-3})\mathbb{P}(T>t_{i-3})\cdots\\ &\cdots\mathbb{P}(T>t_2\,|\,T>t_1)\mathbb{P}(T>t_2\,|\,T>t_1)\mathbb{P}(T>t_1\,|\,T>t_0)\mathbb{P}(T>t_0). \end{split} \] We know that \(\mathbb{P}(T>t_0)\), the probability of the time to the event of interest being more than zero, is one, since the event has not happened to any of our subjects at the start of the study. So by the expression above, we can recursively estimate the survival function \(S(t_{i})\) for each \(t_1,t_2,t_3,\ldots\), using the cumulative product of the conditional probabilities \(\mathbb{P}(T> t_i\,|\,T>t_{i-1})\).
To get an idea of how the Kaplan-Meier method of estimating a survival function works, let’s try it out on some data from a real observational study from the 1980s6. Over two years, a group of obstetricians in London recorded the time it took for a group of 38 women who had been experiencing fertility issues to conceive after a surgical intervention. The times to conception or censoring for each woman can be obtained from a 1998 article on the Kaplan-Meier method in the BMJ7.
women <- 1:38 # creating identifiers for each woman in the study
event_times <- c(1, 1, 11, 7, 3, 4, 9, 4, 24, 6, 9, 2, 6, 16, 9, 2, 2, 3, 1, 8, 8, 4, 4, 1, 7, 9, 2, 9, 24,
1, 1, 9, 13, 10, 3, 2, 3, 2) # inputting the number of months after their surgical intervention
# at which they conceived or were censored
conception_or_censoring <- c('Conceived', 'Conceived', 'Censored', 'Censored', 'Conceived', 'Conceived', 'Censored', 'Conceived', 'Censored', 'Conceived', 'Censored',
'Conceived', 'Conceived', 'Conceived', 'Conceived', 'Censored', 'Conceived', 'Conceived', 'Conceived', 'Censored', 'Censored', 'Conceived',
'Censored', 'Conceived', 'Censored', 'Conceived', 'Conceived', 'Conceived', 'Censored', 'Conceived', 'Conceived', 'Censored', 'Conceived',
'Conceived', 'Conceived', 'Conceived', 'Censored', 'Conceived') # inputting which event occurred for each woman
conception_study <- data.frame(subject=women, months=event_times, event=conception_or_censoring)| Study Participant | ||||||||||||||||||||||||||||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | |
| Event | Conceived | Conceived | Censored | Censored | Conceived | Conceived | Censored | Conceived | Censored | Conceived | Censored | Conceived | Conceived | Conceived | Conceived | Censored | Conceived | Conceived | Conceived | Censored | Censored | Conceived | Censored | Conceived | Censored | Conceived | Conceived | Conceived | Censored | Conceived | Conceived | Censored | Conceived | Conceived | Conceived | Conceived | Censored | Conceived |
| Months Until Event | 1 | 1 | 11 | 7 | 3 | 4 | 9 | 4 | 24 | 6 | 9 | 2 | 6 | 16 | 9 | 2 | 2 | 3 | 1 | 8 | 8 | 4 | 4 | 1 | 7 | 9 | 2 | 9 | 24 | 1 | 1 | 9 | 13 | 10 | 3 | 2 | 3 | 2 |
To make it easier to do our survival analysis, let’s summarise this data so that we can easily see the number of women who conceived or were censored at each distinct time step.
months_from_intervention <- sort(unique(conception_study$months)) # getting the different numbers of months after surgical intervention
# it took for conception or censoring to occur
months_from_intervention <- c(0, months_from_intervention) # adding month zero for the start of the study
num_times <- length(months_from_intervention) # finding the number of unique event times
conception_data_summary <- data.frame(months=months_from_intervention,
censored=rep(NA, times=num_times),
conceived=rep(NA, times=num_times))
for (i in 1:num_times) { # counting the number of conceptions and censorings at each event time
month_i <- months_from_intervention[i]
conception_data_summary$censored[i] <- nrow(conception_study[conception_study$months == month_i & conception_study$event == 'Censored', ])
conception_data_summary$conceived[i] <- nrow(conception_study[conception_study$months == month_i & conception_study$event == 'Conceived', ])
}
Months from
Intervention
|
Number of
Censorings
|
Number of
Conceptions
|
| 0 | 0 | 0 |
| 1 | 0 | 6 |
| 2 | 1 | 5 |
| 3 | 1 | 3 |
| 4 | 1 | 3 |
| 6 | 0 | 2 |
| 7 | 2 | 0 |
| 8 | 2 | 0 |
| 9 | 3 | 3 |
| 10 | 0 | 1 |
| 11 | 1 | 0 |
| 13 | 0 | 1 |
| 16 | 0 | 1 |
| 24 | 2 | 0 |
To calculate the conditional probability \(\mathbb{P}(T>t_i|T>t_{i-1})\) for each observed number of months from conception, \(t_i\), we first need to find out how many women were still being followed up at each stage.
conception_data_summary$remaining <- rep(NA, times=num_times) # initialising a column of our data frame to store the number of remaining study members at each event time
conception_data_summary$remaining[1] <- 38 # at month zero, all women are still being followed up
for (i in 2:num_times) { # finding the number of women still being followed up at each event time from the previous number,
# and the number who conceived or were censored at the previous event time
prev_conceptions <- conception_data_summary$conceived[i-1]
prev_censorings <- conception_data_summary$censored[i-1]
conception_data_summary$remaining[i] <- conception_data_summary$remaining[i-1] - prev_conceptions - prev_censorings
}
Months from
Intervention
|
Number of
Censorings
|
Number of
Conceptions
|
Number of Participants
Still Being Followed
|
| 0 | 0 | 0 | 38 |
| 1 | 0 | 6 | 38 − 0 − 0 = 38 |
| 2 | 1 | 5 | 38 − 0 − 6 = 32 |
| 3 | 1 | 3 | 32 − 1 − 5 = 26 |
| 4 | 1 | 3 | 26 − 1 − 3 = 22 |
| 6 | 0 | 2 | 22 − 1 − 3 = 18 |
| 7 | 2 | 0 | 18 − 0 − 2 = 16 |
| 8 | 2 | 0 | 16 − 2 − 0 = 14 |
| 9 | 3 | 3 | 14 − 2 − 0 = 12 |
| 10 | 0 | 1 | 12 − 3 − 3 = 6 |
| 11 | 1 | 0 | 6 − 0 − 1 = 5 |
| 13 | 0 | 1 | 5 − 1 − 0 = 4 |
| 16 | 0 | 1 | 4 − 0 − 1 = 3 |
| 24 | 2 | 0 | 3 − 0 − 1 = 2 |
Now we can start our survival analysis properly by estimating \(\mathbb{P}(T>t_i\,|\,T>t_{i-1})\) for each \(t_i\). We have gleaned all the information we need from the number of censorings at each time stage, so this column can be removed.
conception_survival_analysis <- subset(conception_data_summary, select=-censored) # creating a new data frame without the censoring column
conception_survival_analysis$conditionals <- with(conception_survival_analysis, (remaining-conceived)/remaining)| \(i\) | \(t_{i}\) (Months) |
\(\#(T = t_{i})\) (Conceptions) |
Number of Study
Participants
|
Estimated \(\mathbb{P}(T > t_{i}\,|\, T > t_{i - 1})\) |
| 0 | 0 | 0 | 38 | \(\text{N/A}\,(\mathbb{P}(T > 0) = 1)\) |
| 1 | 1 | 6 | 38 | \(1 - \frac{6}{38} = \frac{32}{38} \approx 0.84\) |
| 2 | 2 | 5 | 32 | \(1 - \frac{5}{32} = \frac{27}{32} \approx 0.84\) |
| 3 | 3 | 3 | 26 | \(1 - \frac{3}{26} = \frac{23}{26} \approx 0.88\) |
| 4 | 4 | 3 | 22 | \(1 - \frac{3}{22} = \frac{19}{22} \approx 0.86\) |
| 5 | 6 | 2 | 18 | \(1 - \frac{2}{18} = \frac{16}{18} \approx 0.89\) |
| 6 | 7 | 0 | 16 | \(1 - \frac{0}{16} = 1\) |
| 7 | 8 | 0 | 14 | \(1 - \frac{0}{14} = 1\) |
| 8 | 9 | 3 | 12 | \(1 - \frac{3}{12} = \frac{9}{12} = 0.75\) |
| 9 | 10 | 1 | 6 | \(1 - \frac{1}{6} = \frac{5}{6} \approx 0.83\) |
| 10 | 11 | 0 | 5 | \(1 - \frac{0}{5} = 1\) |
| 11 | 13 | 1 | 4 | \(1 - \frac{1}{4} = \frac{3}{4} = 0.75\) |
| 12 | 16 | 1 | 3 | \(1 - \frac{1}{3} = \frac{2}{3} \approx 0.67\) |
| 13 | 24 | 0 | 2 | \(1 - \frac{0}{2} = 1\) |
Finally, we can use these conditional probabilities to estimate \(S(t)\).
conception_survival_analysis$survival <- cumprod(conception_survival_analysis$conditionals) # finding the cumulative product of the estimated conditional probabilities| \(i\) | \(t_{i}\) (Months) |
\(\#(T = t_{i})\) (Conceptions) |
Number of Study
Participants
|
Estimated \(\mathbb{P}(T > t_{i}\,|\, T > t_{i - 1})\) | Estimated \(\mathbb{P}(T > t_{i})\) |
| 0 | 0 | 0 | 38 | \(\text{N/A}\,(\mathbb{P}(T > 0) = 1)\) | \(1\) |
| 1 | 1 | 6 | 38 | \(\frac{32}{38}\) | \(\frac{32}{38} \times 1 = \frac{32}{38} \approx 0.84\) |
| 2 | 2 | 5 | 32 | \(\frac{27}{32}\) | \(\frac{27}{32} \times \frac{32}{38} = \frac{27}{38} \approx 0.71\) |
| 3 | 3 | 3 | 26 | \(\frac{23}{26}\) | \(\frac{23}{26} \times \frac{27}{38} = \frac{621}{988} \approx 0.63\) |
| 4 | 4 | 3 | 22 | \(\frac{19}{22}\) | \(\frac{19}{22} \times \frac{621}{988} = \frac{621}{1144} \approx 0.54\) |
| 5 | 6 | 2 | 18 | \(\frac{16}{18}\) | \(\frac{16}{18} \times \frac{621}{1144} = \frac{69}{143} \approx 0.48\) |
| 6 | 7 | 0 | 16 | \(1\) | \(1 \times \frac{69}{143} = \frac{69}{143} \approx 0.48\) |
| 7 | 8 | 0 | 14 | \(1\) | \(1 \times \frac{69}{143} = \frac{69}{143} \approx 0.48\) |
| 8 | 9 | 3 | 12 | \(\frac{9}{12}\) | \(\frac{9}{12} \times \frac{69}{143} = \frac{207}{572} \approx 0.36\) |
| 9 | 10 | 1 | 6 | \(\frac{5}{6}\) | \(\frac{5}{6} \times \frac{207}{572} = \frac{345}{1144} \approx 0.30\) |
| 10 | 11 | 0 | 5 | \(1\) | \(1 \times \frac{345}{1144} = \frac{345}{1144} \approx 0.30\) |
| 11 | 13 | 1 | 4 | \(\frac{3}{4}\) | \(\frac{3}{4} \times \frac{345}{1144} = \frac{1035}{4576} \approx 0.23\) |
| 12 | 16 | 1 | 3 | \(\frac{2}{3}\) | \(\frac{2}{3} \times \frac{1035}{4576} = \frac{345}{2288} \approx 0.15\) |
| 13 | 24 | 0 | 2 | \(1\) | \(1 \times \frac{345}{2288} = \frac{345}{2288} \approx 0.15\) |
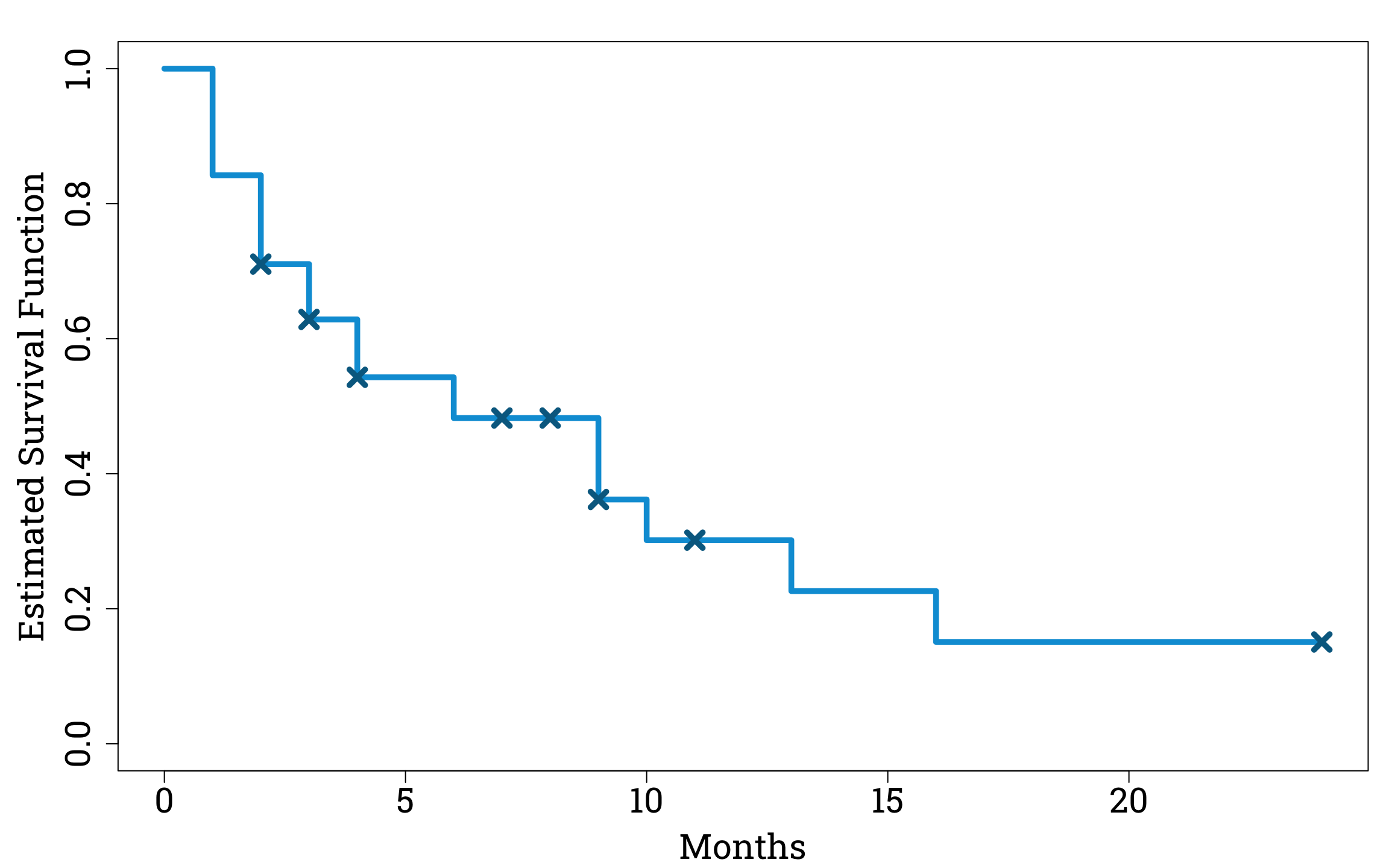
We can now plot our estimate for \(\mathbb{P}(T>t)\) as a stepwise function of \(t\). As is conventional when plotting Kaplan-Meier curves we also mark the months in which censoring occurs.
par(mar=c(bottom=4.2, left=5.1, top=1.8, right=0.9), family="Roboto Slab") # setting the plot options
KM_curve_plot <- function (surv_df, study_df) { # creating a function to plot a survival curve from the
# original data frame and our survival analysis data frame
plot(surv_df$months, surv_df$survival, type="s", ylim=c(0,1),
xlab="Months", ylab="Estimated Survival Function", col="#009ed8", lwd=4.8, cex.lab=1.8, cex.axis=1.8)
censoring_months <- sort(unique(study_df[which((study_df$event == 'Censored')),]$months)) # finding the months in which censoring occurred
surv_fuc_eval_at_censoring <- surv_df[surv_df$months %in% censoring_months,]$survival # evaluating the estimated survival function
# at those points
points(censoring_months, surv_fuc_eval_at_censoring, pch=4, cex=1.8, col="#006a90", lwd=4.8)
}
KM_curve_plot(conception_survival_analysis, conception_study)
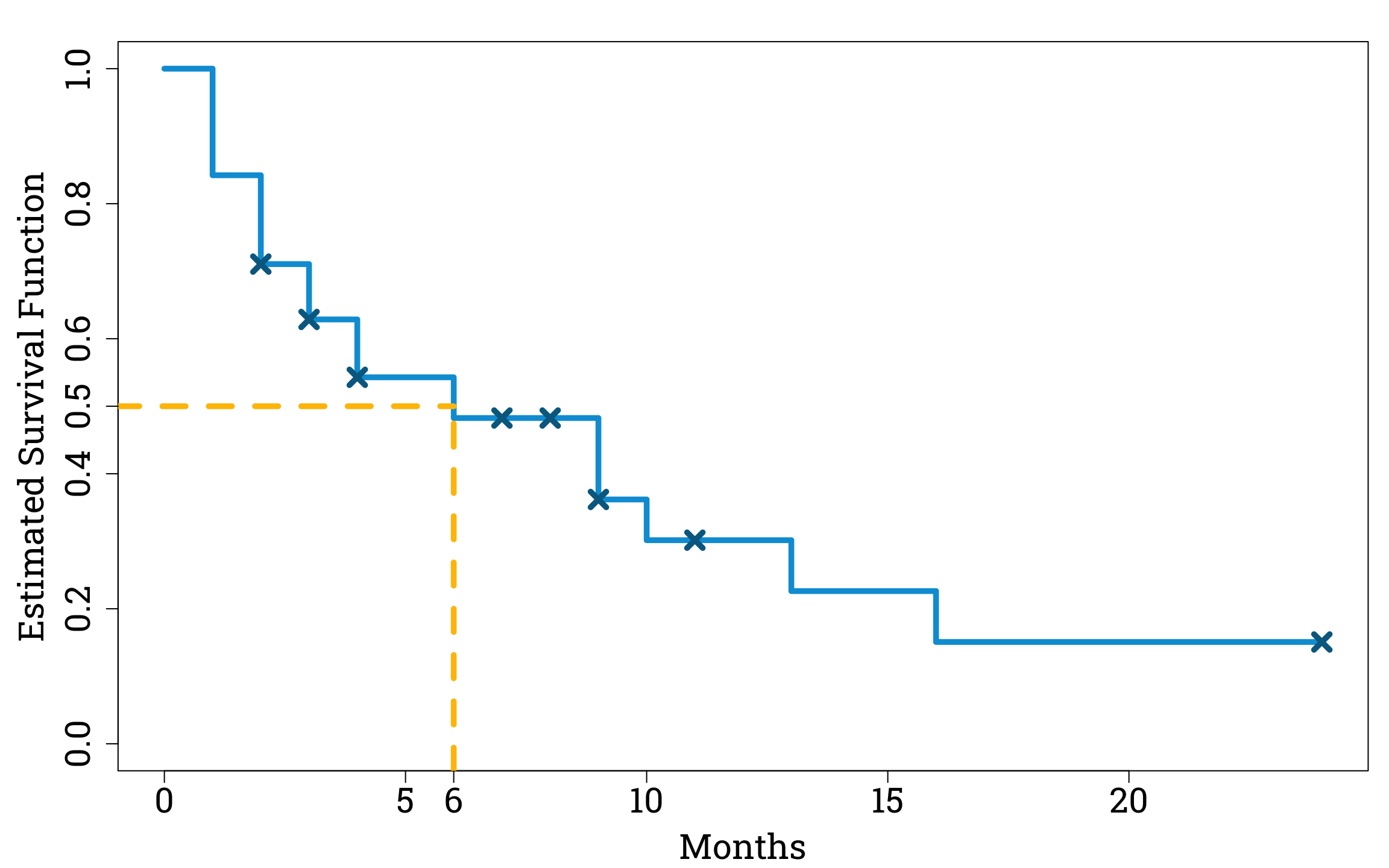
Our estimated survival function allows us to work out a principled estimate for the median time to conception after laparoscopy and hydrotubation. Since the median time it takes to conceive, \(t_m\), is equal to the point where \(\mathbb{P}(T>t_m)=0.5\), we can just draw a line across from 0.5 on the y-axis to our Kaplan-Meier curve.
median_month <- conception_survival_analysis$months[which(conception_survival_analysis$survival <= 0.5)[1]] # finding the first month at which the estimated survival function drops to equal or below 0.5
par(mar=c(bottom=4.2, left=5.1, top=1.8, right=0.9), family="Roboto Slab") # setting the plot options
KM_curve_plot(conception_survival_analysis, conception_study)
segments(-1, 0.5, median_month, 0.5, col="#ffc000", lwd=4.8, lty=2) # plotting the line across from the y-axis to the survival curve
axis(1, at=median_month, cex.lab=1.8, cex.axis=1.8) # marking 0.5 on the y-axis
segments(median_month, -1, median_month, 0.5, col="#ffc000", lwd=4.8, lty=2) # plotting the line down from the survival curve to the x-axis
axis(2, at=0.5, cex.lab=1.8, cex.axis=1.8) # marking the median on the x-axis
We find that the median number of months that passed before women conceived after laparoscopy and hydrotubation was six. So, based on the results of this study, we would expect a woman with the same type of fertility problems as the study participants to have a 50% chance of conceiving within the first six months following laparoscopy and hydrotubation.
Emily Zabor, “Survival Analysis in R,” June 21, 2023.↩︎
Douglas Altman and Martin Bland, “Time to event (survival) data,” BMJ 317, no. 7156 (August 1998): 468–469.↩︎
Vimal Chadha et al., “Tenckhoff catheters prove superior to cook catheters in pediatric acute peritoneal dialysis,” American Journal of Kidney Diseases 35, no. 6 (June 2000): 111–1116.↩︎
Edward Kaplan and Paul Meier, “Nonparametric Estimation From Incomplete Observations,” Journal of the American Statistical Association 53, no. 282 (June 1958): 457–481.↩︎
Richard Van Noorden, Brendan Maher, and Regina Nuzzo, “The Top 100 Papers,” Nature 514, no. 7524 (October 2014): 550–553.↩︎
Paramjit Luthra, Martin Bland, and Stuart Stanton, “Incidence of Pregnancy After Laparoscopy and Hydrotubation,” British Medical Journal (Clinical Research Edition) 284, no. 6321 (April, 1982): 101.↩︎
Martin Bland and Douglas Altman, “Survival probabilities (the Kaplan-Meier method),” BMJ 317, no. 7172 (December 1998): 1572.↩︎