This article was written solely for informational and educational purposes, and does not constitute medical advice. If you have any health concerns, please consult a qualified medical professional.
Thousands of kidney transplants are performed every year in the UK, transforming the lives of their recipients. In this article, I’ll explore how techniques from the mathematical discipline of graph theory help to facilitate some of these transplants.
Some Graph Theory Background
Suppose that you are a teacher in charge of taking a group of six students, who we will call Students A, B, C, D, E, and F, on a school trip, and you need to decide what pairs they are going to sit in on the minibus. You ask the students to anonymously let you know who they would be willing to sit with and find out that:
- Student A and Student D would be happy to be in a pair.
- Student A and Student E would be happy to be in a pair.
- Student A and Student F would be happy to be in a pair.
- Student B and Student C would be happy to be in a pair.
- Student B and Student E would be happy to be in a pair.
- Student C and Student D would be happy to be in a pair.
We can represent this information in a graph, which, in discrete mathematics, means a structure consisting of vertices and edges (as opposed to describing a chart or a plot).
Here, the points of the graph – their vertices (sometimes also called nodes) – represent the students, and the lines between the vertices, known as edges, encode the possible pairings they can sit in; if two students would accept being seated together, they have an edge between them. Graphs are commonly used to study community structures in sociology, and they can also be applied to protein-protein interaction networks in biology and transportation networks in urban planning, to give just two other examples.
Graphs can be represented computationally in several different ways; here, we will discuss three of the most common – adjacency matrices, adjacency lists, and edge lists. For a graph \(G\) with \(n\) vertices, the adjacency matrix of \(G\) is an \(n\times n\) matrix \(A_G\), where the entry in row \(i\) and column \(j\) of \(A_G\) is \(1\) if vertex \(i\) and vertex \(j\) are connected by an edge, and \(0\) if they are not. For the rest of this article, we will denote the specific graph structure above, representing the possible seating arrangements of the students, by \(S\). The adjacency matrix for \(S\) is
\[
A_S=
\begin{pmatrix}
0 & 0 & 0 & 1 & 1 & 1 \\
0 & 0 & 1 & 0 & 1 & 0 \\
0 & 1 & 0 & 1 & 0 & 0 \\
1 & 0 & 1 & 0 & 0 & 0 \\
1 & 0 & 0 & 0 & 0 & 0
\end{pmatrix}.
\]
Defining the Adjacency Matrix for \(S\) in R
S_adj_mat <- matrix(c(# Let's walk through how we fill out the first row of the adjacency matrix:
# Row 1 represents the people Student A can sit with;
# they form a compatible pair with Students D, E, and F,
# so there is a 1 in column 4, representing Student D,
# a 1 in column 5, representing Student E,
# and a 1 in column 6, representing Student F.
# The pairings A-B and A-C are unacceptable so there are 0s in columns 2 and 3.
# Vertex A is not connected to itself, because Student A cannot form a pair with themselves,
# so there is a 0 in column 1 – in fact, all the diagonal values of this adjacency matrix are 0
# because none of the vertices have edges connecting them to themselves.
0, 0, 0, 1, 1, 1,
0, 0, 1, 0, 1, 0,
0, 1, 0, 1, 0, 0,
1, 0, 1, 0, 0, 0,
1, 1, 0, 0, 0, 0,
1, 0, 0, 0, 0, 0),
nrow = 6, byrow = TRUE)
As well as an adjacency matrix \(M\) for \(G\), we can also create an adjacency list, \(L_G\), which is a list of length \(n\), where each entry is also a list. The \(i\)th element of \(L_G\) is a list of vertices that vertex \(i\) of graph \(G\) forms an edge with – this list can have a length of zero if vertex \(i\) is not connected to any vertices.
Finding \(L_S\) from \(A_S\) in R
# Let's write a function which takes as its input a graph's adjacency matrix, and returns the adjacency list for the graph
adj_mat_to_adj_list <- function(adj_mat){
num_nodes <- ncol(adj_mat) # we find the number of vertices of the graph
adjacency_list <- vector(mode = "list", length = num_nodes) # we initialise our adjacency list as an empty list with the same number of elements of vertices of the graph
# Now we make an empty list for each vertex and fill it with the indexes of the vertices that it is connected to:
for (i in 1:num_nodes){
connected_vertices <- list()
for (j in 1:num_nodes) {
if (adj_mat[i,j] == 1) {
connected_vertices <- c(connected_vertices, j)
}
}
adjacency_list[[i]] <- connected_vertices
}
adjacency_list
}
# We can use this function to find the adjacency list for S:
S_adj_list <- adj_mat_to_adj_list(S_adj_mat)
names(S_adj_list) <- c("A","B","C","D","E","F")
cat("Vertex 1 (A):", LETTERS[unlist(S_adj_list$A)],
"\nVertex 2 (B):", LETTERS[unlist(S_adj_list$B)],
"\nVertex 3 (C):", LETTERS[unlist(S_adj_list$C)],
"\nVertex 4 (D):", LETTERS[unlist(S_adj_list$D)],
"\nVertex 5 (E):", LETTERS[unlist(S_adj_list$E)],
"\nVertex 6 (F):", LETTERS[unlist(S_adj_list$F)])
Vertex 1 (A): D E F
Vertex 2 (B): C E
Vertex 3 (C): B D
Vertex 4 (D): A C
Vertex 5 (E): A B
Vertex 6 (F): A
Finally, we can also create an ‘edge list’, \(E_G\), of all the edges of \(G\).
Finding \(E_S\) from \(A_S\) in R
# We can write a simple function to get the edge list matrix of a graph from it's adjacency matrix:
adj_mat_to_edge_list <- function(adj_mat) {
# We can represent each edge as a vector of length two where the elements are the vertices
# that the edge is connected to, and thus encode the edge list as a two column matrix
edge_list <- unique(t(apply(which(adj_mat == 1, arr.ind = TRUE), 1, sort)))
edge_list
}
# Let's see what the output looks like for S:
S_edge_list <- adj_mat_to_edge_list(S_adj_mat)
# We can convert the vertex numbers to letters to check we've got the result we've expected:
letters_edge_list <- apply(S_edge_list, 1:2, function(i) LETTERS[i])
for (i in 1:nrow(letters_edge_list)) {
cat(letters_edge_list[i,1], "–", letters_edge_list[i,2], ",\n", sep = "")
}
A–D,
A–E,
A–F,
B–C,
B–E,
C–D,
Now that we know some definitions, we can return to our problem – finding a configuration in which the maximum possible number of passengers on the minibus are happy with their partner. Each person can only sit with one other person, so in graph theory terms we are looking to find a matching of the graph – this is a set of edges of the graph in which no two edges share any common vertices. But it’s not enough just to find any matching – for example the set of edges \(\{\)A–D\(\}\) is a matching, as is the set \(\{\)C–D\(\}\), but neither are very useful to us as they both only give us one pairing.
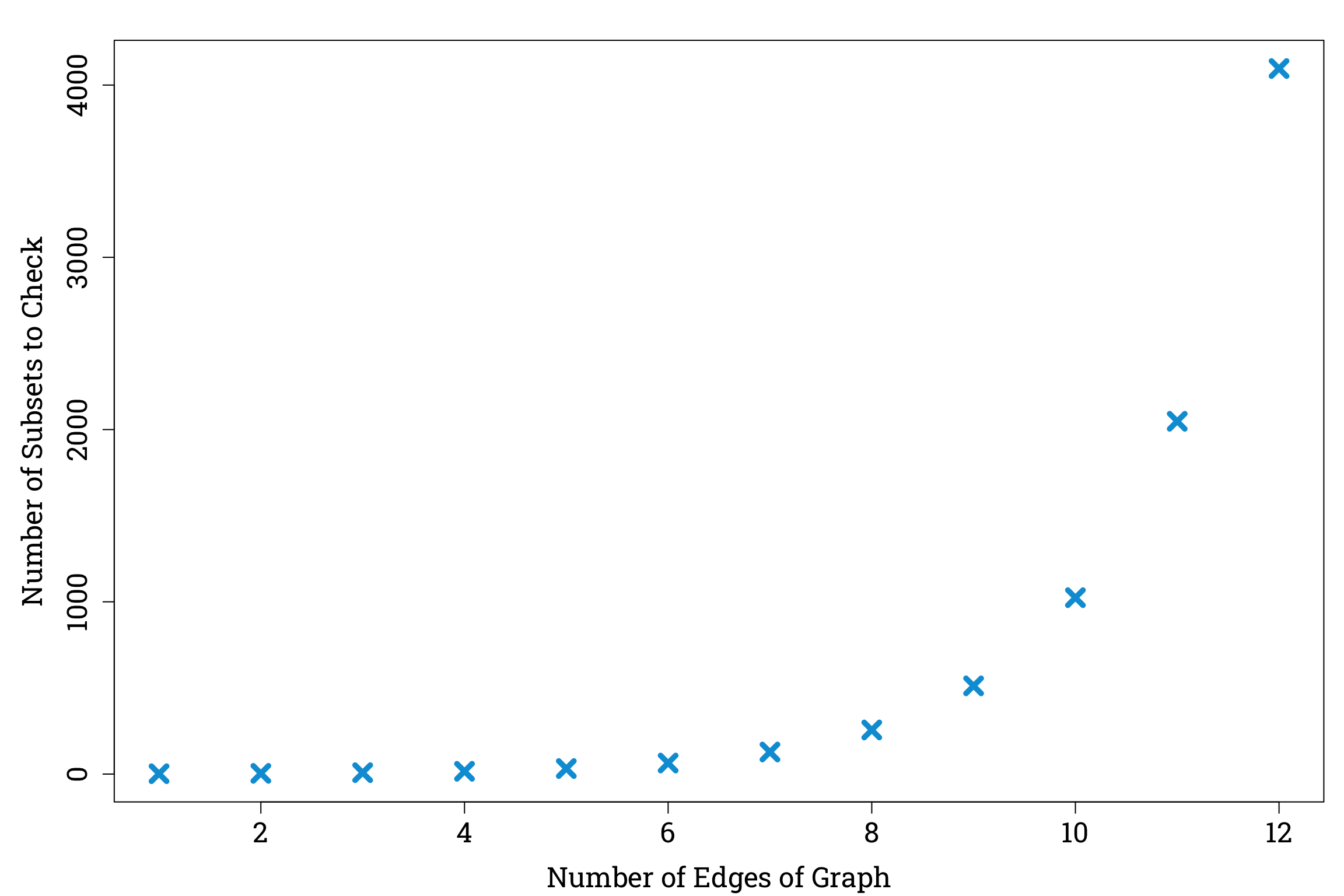
Instead, we are looking for a maximum matching, which is a matching of a graph that has the largest possible number of edges. One way to find a maximum matching of a graph \(G\) would be to check all the possible subsets of edges of \(G\), throw out the ones that aren’t matchings, and then pick the largest remaining subset. But since the set of all possible subsets of edges is equal to the power set of the set of edges of \(G\), it contains \(2^{E}\) subsets for us to check, where \(E\) is the number of edges of \(G\). For our graph \(S\), this would give us \(2^6=64\) subsets to check, which might just about be manageable, but as the number of edges increases, the number of subsets we will need to check using this naive approach will grow exponentially. A graph with 12 edges, for example, would require us to check \(2^{12}=4096\) subsets!
Plotting the Number of Subsets of Edges Against the Number of Edges in R
par(mar=c(bottom=4.2, left=5.1, top=1.8, right=0.9), family="Roboto Slab") # setting the plot options
num_edges <- 1:12
plot(num_edges, 2^num_edges, pch=4, cex=1.8, lwd=4.8, col="#009ed8",
xlab="Number of Edges of Graph", ylab="Number of Subsets to Check",
cex.lab=1.5, cex.axis=1.5)
To understand the algorithms that allow us to find a maximum matching more quickly, we need another concept from graph theory – augmenting paths. Given a graph \(G\), and a matching \(M\), an augmenting path is a sequence of edges, \(P\), that connect two unmatched vertices of \(G\) such that the edges \(P\) are alternately in \(M\) and not in \(M\). For example, if we have graph with four vertices and an edge list 1–2, 2–3, 3–4 and we are given a matching 2–3, the augmenting path is 1–2, 2–3, 3–4.
Writing a Function that Will Find an Augmenting Path for a Given Graph and Matching in R
augmenting_path <- function(adj_list, match_vec) {
# This function takes as input the edge list of the graph, and a vector, `match_vec` which represents the matching.
# The length of `match_vec` should be the same as the number of vertices of the graph, and `match_vec[i]` is the index
# of the vertex that the $i$th vertex is matched to – if it is unmatched then we'll define `match_vec[i]` to be zero.
vertices_match_status <- match_vec != 0 # we create a logical vector to represent whether each vertex is included in the matching
num_vertices <- length(vertices_match_status) # we find the number of vertices in the graph
unmatched_vertices <- which(vertices_match_status == FALSE, arr.ind=TRUE) # we create a vector of the vertices which are not in the matching
for (i in 1:num_vertices) { # we will try finding an augmenting path starting from each unmatched vertex until we find one
aug_path <- matrix(, nrow=0, ncol=2) # we initialise an empty matrix to start the augmenting path
if (vertices_match_status[i] == TRUE) { # we skip the matched vertices
next
}
root <- i
current_vert <- i # we will use this variable to keep track of which vertex we have reached
# in our attempt to find an augmenting path
# Let's keep track of the vertices we've included in our augmenting path attempt from this vertex:
unvisited_from_root <- c(1:num_vertices)
unvisited_from_root <- unvisited_from_root[!unvisited_from_root==root]
repeat { # we create a repeating loop that will run the same procedure
# until we break out of it using break or return
neighbours <- unlist(adj_list[[current_vert]]) # we create a vector of the vertices that have an edge
# between them and the vertex that we are currently on
neighbours_unvisited_from_root <- intersect(neighbours, unvisited_from_root) # we create a vector of vertices
# adjacent to the vertex we are
# currently on that have not already
# been included in our attempt to
# find an augmenting path
if (length(neighbours_unvisited_from_root) == 0) { # if there are none of these, we can stop running our repeat loop
# and try our search again from the next unmatched vertex
break
}
match_to_current_vert <- match_vec[current_vert]
# if we are on a vertex that is part of the matching, and the vertex it is matched
# to is not yet part of the augmenting path, we want to go to that vertex next
if (match_to_current_vert %in% unvisited_from_root) {
next_vert <- match_to_current_vert
unvisited_from_root <- unvisited_from_root[!unvisited_from_root==next_vert]
aug_path <- rbind(aug_path, c(current_vert,next_vert))
current_vert <- next_vert
next
}
unmatched_neighbours_unvisited_from_root <- intersect(unmatched_vertices, neighbours_unvisited_from_root) # we create a vector of unmatched vertices
# adjacent to the vertex we are currently
# on that we haven't already included in our
# augmenting path attempt
if (length(unmatched_neighbours_unvisited_from_root) > 0) { # if any of these exist, then we have found an augmenting path, and we can return it!
aug_path <- rbind(aug_path, c(current_vert,unmatched_neighbours_unvisited_from_root[1]))
return(aug_path)
}
# If we didn't return an augmenting path in the if statement above,
# all the vertices adjacent to the vertex we are currently on that
# are not already included in our augmenting path attempt must be part
# of the matching, so we will go to one of these next and continue searching:
next_vert <- neighbours_unvisited_from_root[1]
unvisited_from_root <- unvisited_from_root[!unvisited_from_root==next_vert]
aug_path <- rbind(aug_path, c(current_vert,next_vert))
current_vert <- next_vert
}
}
# If we haven't returned an augmenting path after searching from all unmatched vertices, we return an empty matrix:
aug_path <- matrix(, nrow=0, ncol=2)
return(aug_path)
}
In 1957, mathematician Claude Berge formally proved that if an augmenting path cannot be found for a graph and a matching, then that matching is a maximum matching. This fact had previously been observed by Dénes König, a pioneer of discrete mathematics who published the first ever textbook on the subject of graph theory. König’s book inspired another mathematician, Harold Kuhn, to propose an algorithmic solution to the maximum matching problem.
Kuhn’s algorithm works by starting with any matching on a graph (including an empty matching) and searching the graph from each unmatched vertex until it finds an augmenting path. It then finds the symmetric difference of the path and the current matching, and this set of edges becomes the new, improved matching that it will use for its next iteration. For example, in the scenario above where we have a graph with edge list 1–2, 2–3, 3–4 and a matching 2–3, the first iteration of the algorithm will find the augmenting path 1–2, 2–3, 3–4, and will update the matching to be 1–2, 3–4.
When it can no longer find any augmenting paths, Kuhn’s algorithm terminates, and thanks to Claude Berge’s proof, we can be sure that the matching it has found is a maximum matching.
Coding Kuhn’s algorithm in R
# Let's use our augmenting_path function to write an implementation of Kuhn's algorithm
# that takes as its input the adjacency matrix of a graph and a matching vector:
maximum_matching <- function(adj_mat, match_vec) {
adj_list <- adj_mat_to_adj_list(adj_mat) # we use the function we wrote earlier
num_vertices <- length(match_vec) # we find the number of vertices in the graph
# Let's create a matrix to store the current matching:
current_matching <- matrix(, nrow=0, ncol=2)
# We can populate it with the initial matching to start with:
for (i in 1:num_vertices) {
if (match_vec[i] == 0) {
next
}
current_matching <- rbind(current_matching, c(i,match_vec[i]))
}
if (nrow(current_matching) != 0) {
current_matching <- unique(t(apply(current_matching, 1, sort))) # we order the edges with the lower indexed vertex first,
# and remove duplicates
}
# Now we will run our augmenting path algorithm and and use it to increase our current matching
# until no more augmenting paths can be found:
current_match_vec <- match_vec
repeat {
aug_path <- augmenting_path(adj_list, current_match_vec) # we find an augmenting path for the input graph and the current matching
aug_path_length <- nrow(aug_path)
# If the augmenting_path function has not found any augmenting paths, we break out of the repeat loop:
if (aug_path_length == 0) {
break
}
aug_path <- t(apply(aug_path, 1, sort)) # we order the edges in the augmenting path with the lowest indexed vertex first
# If the augmenting path consists of only one edge,
# we add that edge to our matching and run another iteration
# of the augmenting_path function with the new matching:
if (aug_path_length == 1) {
current_matching <- rbind(current_matching, aug_path)
# Before running the augmenting_path function again
# we need to update the current_match_vec algorithm
# to reflect our new matching:
current_matching_length <- nrow(current_matching)
current_match_vec <- rep(0,num_vertices)
for (i in 1:current_matching_length) {
current_match_vec[current_matching[i,1]] <- current_matching[i,2]
current_match_vec[current_matching[i,2]] <- current_matching[i,1]
}
next
}
# If the augmenting path has more than one edge, we add the edges that are not included in the current matching,
# and remove the ones that are (by the definition of an augmenting path, these alternate):
for (i in 1:aug_path_length) {
if (i%%2 == 1) {
current_matching <- rbind(current_matching, aug_path[i,])
}
if (i%%2 == 0) {
current_matching <- current_matching[!(current_matching[,1]==aug_path[i,1] & current_matching[,2]==aug_path[i,2]),]
}
}
# Before running the augmenting_path function again we need to update the current_match_vec algorithm to reflect our new matching:
current_matching_length <- nrow(current_matching)
current_match_vec <- rep(0,num_vertices)
for (i in 1:current_matching_length) {
current_match_vec[current_matching[i,1]] <- current_matching[i,2]
current_match_vec[current_matching[i,2]] <- current_matching[i,1]
}
}
return(current_matching[order(current_matching[,1]),]) # we return the first matching we arrived at for which no augmenting paths
# could be found, with the edges ordered by their lowest indexed vertex
}
What does this algorithm give us when applied to our example graph \(S\), and an empty matching?
Applying Kuhn’s Algorithm to \(S\) in R
S_empty_matching <- rep(0,6)
S_max_matching <- maximum_matching(S_adj_mat, S_empty_matching)
letters_matching <- apply(S_max_matching, 1:2, function(i) LETTERS[i])
for (i in 1:nrow(letters_matching)) {
cat(letters_matching[i,1], "–", letters_matching[i,2], ",\n", sep = "")
}
So students A and F, B and E, and C and D, can all sit in pairs.
This may seem like something we could have worked out easily by hand, but matching algorithms are really useful when there are so many vertices and edges to a graph that a human could never work out a maximum matching just from looking at it.
You may be relieved to learn that we are nearly at the end of the background graph theory I wanted to include in this article before discussing matching algorithms’ applications to kidney transplants! However, before we move on, I should admit that I have been oversimplifying things somewhat. Though Kuhn’s algorithm will work on a huge variety of graphs, there are some graphs that will trip it up. For example, consider the graph and matching below, taken from this stack exchange post by Misha Lavrov.
Trying to find an augmenting path from vertex 1, the algorithm will go from 1 to 2 to 8 to 9 to 10, before getting stuck and concluding that there is no augmenting path, and thus that the given matching is a maximum matching. Similarly, if it starts from vertex 4 it will follow the sequence of edges 4–3, 3–7, 7–6, 6–5 before it again gets stuck and terminates.
Graphs that run into these kinds of problems are always non-bipartite, meaning they contain cycles of odd numbers of edges, like the pentagons in the graph above. To ensure that, if they exist, augmenting paths can always be found in these types of graph, Kuhn’s algorithm needs to be modified. The first person to find a way to do this was computer scientist Jack Edmonds, who introduced an ingenious method for adapting the algorithm to deal with odd length cycles in his ‘blossom’ algorithm in 1965. The details of his algorithm are fascinating, but beyond the scope of this article, which is why I have only used bipartite graphs as examples, and will continue to do so in the next section. If you want to learn how a maximum matching can be found for any graph using Edmonds’ blossom algorithm, I recommend this excellent youtube video by Tomáš Sláma.
How Matching Algorithms Apply to Kidney Transplants
People with end-stage renal disease have kidneys that are unable to perform their function of filtering the blood and are therefore unable to survive without undergoing regular dialysis, unless they receive a working kidney transplant from a donor. Many people with this condition will have a family member or loved one who is willing to donate a kidney to them – as most of us only need one working kidney to live a healthy life – but this is often not possible due to a mismatch between the donor and the intended recipient’s blood and/or antigen type. For example, imagine that a patient with advanced chronic kidney disease, who we’ll call Recipient A, has a sibling, Donor A, who is willing to donate a kidney to them but cannot because they have incompatible blood groups. In the past, this would have meant that Donor A would have been unable to donate a kidney in order to help their sibling. Nowadays, however, the pair have another option; they can participate in the UK Living Kidney Sharing Scheme. Suppose another recipient and donor pair, a parent and child, say, are in the same situation. If the donor in this pair – for reasons that will shortly become clear, let’s call them Donor F – is a match with Recipient A, and Donor A’s kidney is compatible with the recipient, Recipient F, then the two pairs can effectively ‘swap’ kidneys, in what is called a paired exchange.

We can represent possible paired kidney exchanges between pairs of donors and recipients in a graph, with each vertex representing one incompatible pair, and an edge linking two pairs signifying that a paired exchange is possible between them. Consider the scenario described above; this would be represented by a graph with two vertices and one edge, A–B.

What happens if we introduce more incompatible pairs of donors and recipients? Well, we might end up with a graph like \(S\), but this time with the vertices representing patients in need of kidneys and loved ones who are unable to denote to them. In reality a graph of incompatible donor-recipient pairs in a country like the UK would have hundreds of vertices, but we can use a smaller one to help us think about the problem of matching compatible pairs.
As we saw earlier, several different matchings of this graph exist, but some of them will result in more people receiving kidneys than others. For example, if the Pair A’s transplant centre search a regional or national database for a pair that Pair can exchange a kidney with and stop at the first one they find, then Pair A might be matched with Pair D. This would leave Pair B and Pair C free to participate in a paired exchange, but Recipients E and F would then be left without a kidney. If a maximum matching algorithm is used on the other hand, all six recipients will be matched with a compatible donor.
In 2004, a team from John Hopkins Hospital in the US proposed using Edmonds’ blossom algorithm to optimize kidney exchanges. They used simulated pools of donor-recipient pairs to test their scheme, and found that it would result in more transplants, with better antigen matches, than the ‘first-accept’ system that was in use at the time. Of course, employing an algorithm to decide who gets which organs presents numerous ethical and logistical challenges. For instance, what happens when there is more than one possible maximum matching, resulting in different people getting kidney transplants? Consider what our example graph would look like if we discovered that Recipient B was actually not compatible with Donor E.
This graph has no perfect matching – one in which all vertices are matched – but it does have two different maximum matchings; the matching A–D, B–C and the matching A–F, C–D.
Which kidney transplants should be performed? Should Recipients E and F or Recipients B and E have to remain on dialysis longer as they wait for the next run of the matching algorithm to be performed, or for a suitable deceased donor to match with them? Should the amount of time the recipients have spent on the waiting list for a kidney factor into this decision? What about their ages or levels of frailty? These are difficult questions that no computer can answer for us.
We should also note that compatibility between donors and recipients is not actually as binary as ‘a match’ or ‘not a match’. There are six antigens which are particularly important in organ transplantation and it is rare that donors and recipients will have the same type of each of them, but more antigens in common are still better than fewer. The difference between a donor’s and recipient’s age, as well as whether the recipient has been sensitised to certain antigens by pregnancy or a previous transplant, or a blood transfusion, can also influence the chances of success.
Despite these important concerns, Edmonds’ blossom algorithm is an integral part of the process that NHS Blood and Transplant uses to find possible kidney paired exchanges in the UK. However, it is not the only method used, but is instead embedded as a step within a larger algorithm, developed in conjunction with computer scientists at the University of Glasgow. As well as finding the largest possible matching, their procedure seeks to maximise the total ‘weight’ of a matching, where the weights given to edges of the graph are calculated by a scoring system used by NHSBT that takes into account:
- The number of previous matching runs the recipients have participated in (matching runs take place every three months).
- How sensitised the recipients are to foreign antigens.
- How well matched donor and recipients’ antigens are.
- The age difference between donors and recipients.
Two additional ways in which the algorithm used by NHS Blood and Transport differs from a straightforward implementation of Edmond’s Blossom algorithm are its support for non-directed altruistic donations and its ability to facilitate 3-way exchanges. If you would like to understand how this is done, I recommend the article written by Dr David Manlove of the University of Glasgow on his and his colleagues work on the algorithm used by the UK Living Kidney Sharing Scheme in edition 475 of the London Mathematical Society Newsletter.